Torre de San Miguel
Análisis compositivo
Para el análisis de este edificio, a través del cual demostraremos que el mismo pertenece al proyecto, original y unitario (finales del s. VIII o inicios del IX, del conjunto catedralicio ovetense, aplicaremos nuestra habitual metodología de matriz modular, a la planta cuadrada que la define como una estructura turriforme, a la que, posteriormente, se adosaría la Cámara Santa .
La planta de la torre se deduce de su análisis en alzado, ya que, a nivel terreno, ha desaparecido totalmente su lado O., derribado a finales del s. XV a fin de habilitar un acceso al nuevo transepto Gótico desde el Tránsito de Santa Bárbara, conservándose, no obstante, a partir de los 3 m de altura, y hasta el alzado total de la torre, de unos 36 pies (alero del primitivo tejado a dos aguas, hoy día modificado).
La planta así definida participa de la referencia geométrica de trazado conocida como proporción cierta pura (la planta constituye un cuadrado), pudiendo, no obstante, interpretarse la articulación de su alzado en función de la proyección de la diagonal de dicho cuadrado
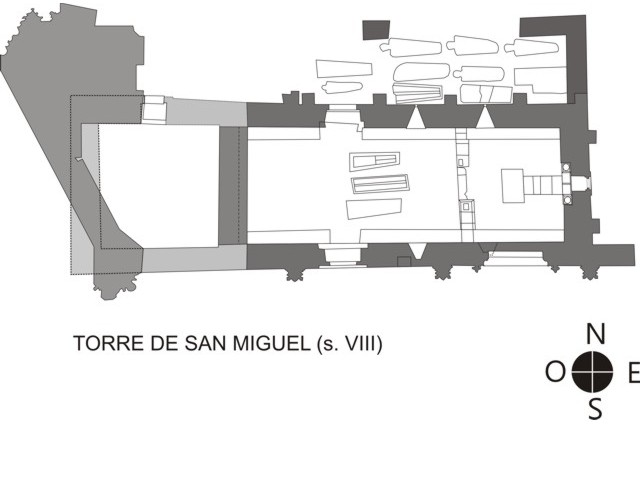
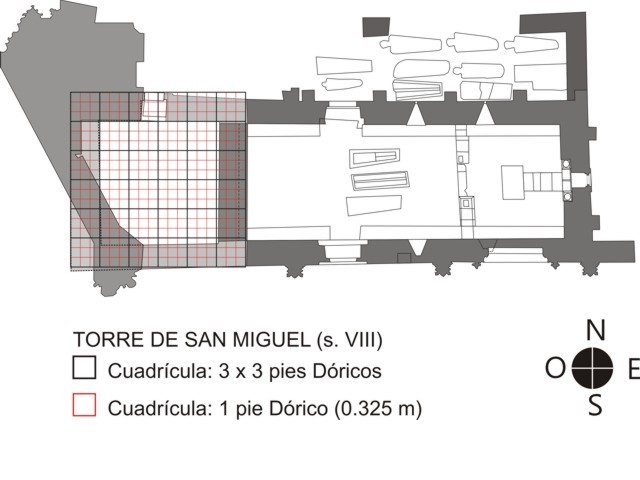
Aplicando al lado de la torre, de unos 5,85 m (Cuenca, J. y Hevia, C.; 1999), el pie dórico-gálico (0.325-0.326 m), resulta una cuadrícula de 18 x 18 pies, que define la planta del edificio, permitiendo articulaciones del espacio del mismo a base de ulteriores subdivisiones.
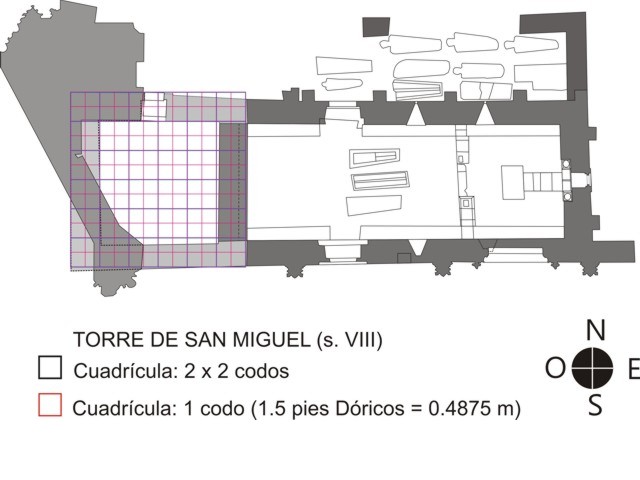
También resulta explicable dicha planta en función del Codo "cvbitvs", equivalente a 1.5 pies, con lo que 2 codos equivaldrían a 3 pies, y la planta total a 12 codos.
Aplicando a la cuadrícula total una matriz modular impar de 3 pies, o par de 2 codos, obtenemos una nueva cuadrícula total de 6 x 6, que define el grosor de los muros de la torre (3 pies equivalentes a 2 codos), así como el espacio interior de la misma (12 pies equivalentes a 8 codos).



Aplicando la cuadrícula en alzado obtenemos un valor de 36 pies, equivalentes a 24 codos, hasta el inicio de la pendiente del tejado primitivo (que pudo ser a 2 o cuatro aguas), que hoy se encuentra reformado a un agua con vertiente hacia el E, donde se ubica la Cámara Santa.

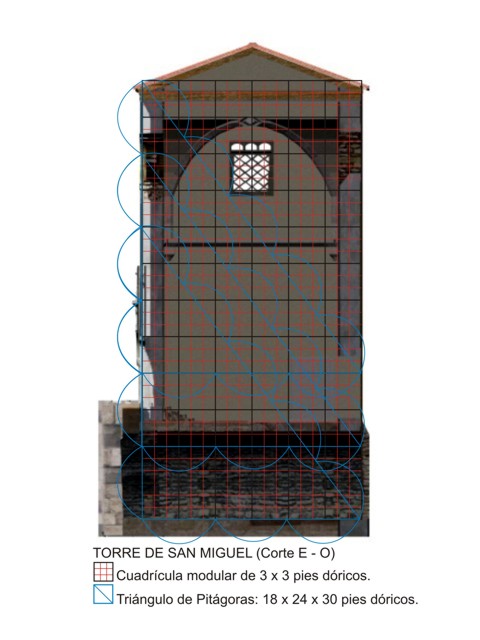
Por el interior, la torre de San Miguel presenta hoy día una configuración bastante diferente a la que, probablemente, exhibió en el momento fundacional de la misma. La triangulación del corte del edificio desde el S. nos permite, al menos, vislumbrar la posibilidad de cuál sería su primitiva configuración.
En efecto se puede explicar el alzado del edificio a través del triángulo de Pitágoras de 18 x 24 x 30 pies utilizado en la articulación de la vecina Iglesia Mayor de San Salvador, mediante tres triángulos superpuestos 6 pies uno sobre otro: el primero nos proporcionaría el nivel del suelo primitivo de la planta principal de la torre, situado a 6 pies, 2 pies por debajo del actual, elevado al construirse la bóveda que abrió el primitivo sótano de la torre a la Cámara Santa; El segundo nos definiría el alzado total de la habitación principal de la torre, diáfana, de unos 24 pies , para la que no puede excluirse, en nuestra opinión, un uso como santuario, y que nos atrevemos a poner en relación con el depósito en ella del Arca Santa; el tercer triángulo definiría el alzado total de 36 pies hasta el plano de la pendiente del tejado, restando 6 pies (más la altura definida por el piñón del tejado), sobre la anteriormente mencionada habitación principal, como ático de la torre.
Análisis metrológico
Partiendo de los resultados obtenidos en el análisis compositivo, aplicando al módulo compositivo obtenido asociado a las dimensiones de su planta cuadrada, de 5.86 m (M = 5.86 m, 18 pies o 12 codos), una matriz modular impar, en función del pie, o par, en función del codo, de valores respectivos 3 (M = 6 x 3 x 1/6M) y 2 (M = 6 x 2 x 1/6M); determinamos, en hipótesis, un valor para cada cuadrícula de 1/18M de 0.326 m, equivalente a 1 pie, o de 1/12 M de 0.489 m, basada, en ambos casos, en el denominado "Pie dórico", utilizado en nonumentos de la Grecia clásica (Dörpfeld, 1935), y que preside, según lo que vamos viendo en el análisis de los principales templos, el proyecto unitario del conjunto religioso ovetense. A partir de la cuadrícula asociada a esta dimensión modular concreta se explican las dimensiones de las principales partes orgánicas del edificio (ver figuras del análisis compositivo), y se constata de nuevo que existen dimensiones en la arquitectura altomedieval asturiana que, al igual que en la romana, responden a convenciones establecidas, de las cuales la más patente es el ancho de los muros , que, en este caso, alcanza los dos codos, o tres pies, un pie más de lo habitual, lo cual puede venir determinado por el carácter turriforme del edificio.
Las conclusiones observadas en la aplicación de tal unidad de medida al edificio, en planta, las expresamos en los cuadros siguientes:
| METROS | PASSVS | GRADVS | CVBITVS | PALMIPES | PES | PALMVS | |
|---|---|---|---|---|---|---|---|
| LONGITUD | 5,868 | 3,600 | 7,200 | 12,000 | 14,400 | 18,000 | 72,000 |
| ANCHURA | 5,868 | 3,600 | 7,200 | 12,000 | 14,400 | 18,000 | 72,000 |
| METROS | PASSVS | GRADVS | CVBITVS | PALMIPES | PES | PALMVS | |
|---|---|---|---|---|---|---|---|
| MÓDULO | 5,868 | 3,600 | 7,200 | 12,000 | 14,400 | 18,000 | 72,000 |
| 1/3 MÓDULO | 1,956 | 1,200 | 2,400 | 4,000 | 4,800 | 6,000 | 24,000 |
| 1/6 MÓDULO | 0,978 | 0,600 | 1,200 | 2,000 | 2,400 | 3,000 | 12,000 |
| METROS | MÓDULO | 1/3 MÓD. | 1/6 MÓD. | PASSVS | GRADVS | CVBITVS | PALMIPES | PES | PALMVS | |
|---|---|---|---|---|---|---|---|---|---|---|
| FACHADA (hasta pte. del tejado | 11,736 | 2,000 | 6,000 | 12,000 | 7,200 | 14,400 | 24,000 | 28,800 | 36,000 | 144,000 |
| METROS | MÓDULO | 1/3 MÓD. | 1/6 MÓD. | PASSVS | GRADVS | CVBITVS | PALMIPES | PES | PALMVS | |
|---|---|---|---|---|---|---|---|---|---|---|
| ANCHO DE MUROS (piso bajo) | 0,978 | 0,167 | 0,500 | 1,000 | 0,600 | 1,200 | 2,000 | 2,400 | 3,000 | 12,000 |
| INTERIOR (piso bajo) | 3,912 | 0,667 | 2,000 | 4,000 | 2,400 | 4,800 | 8,000 | 9,600 | 12,000 | 48,000 |
| MEDIDA | EQUIVALENCIAS | En m | |||||||
|---|---|---|---|---|---|---|---|---|---|
| DECEMPEDA | 1 | 3,260 | |||||||
| PASSVS | 2 | 1 | 1,630 | ||||||
| GRADVS | 4 | 2 | 1 | 0,815 | |||||
| CVBITVS | 6,67 | 3,34 | 1,67 | 1 | 0,489 | ||||
| PALMIPES | 8 | 4 | 2 | 1,2 | 1 | 0,408 | |||
| PES | 10 | 5 | 2,5 | 1,5 | 1,25 | 1 | 0,326 | ||
| SEMIS | 20 | 10 | 5 | 3 | 2,5 | 2 | 1 | 0,163 | |
| PALMVS | 40 | 20 | 10 | 6 | 5 | 4 | 2 | 1 | 0,082 |